Rede Neural Atômica: nova perspectiva inspirada no Modelo Atômico de Rutherford para Aprendizado XOR
- #Machine Learning
- #Python
Resumo
Este artigo tem como objetivo apresentar uma nova arquitetura de rede neural inspirada no modelo atômico de Rutherford. A ideia consiste em organizar os neurônios em um núcleo central e camadas orbitais concêntricas, simulando o comportamento dos elétrons orbitando o núcleo. Submetemos a rede ao clássico problema XOR, demonstrando que a arquitetura é capaz de aprender funções não lineares simples, oferecendo uma analogia visual e conceitual para compreensão do fluxo de informação desejado em redes neurais.
1. Introdução
Redes neurais artificiais são modelos computacionais inspirados no funcionamento do cérebro humano. Um dos benchmarks clássicos é o problema XOR, que demonstra a necessidade de redes com camadas ocultas para capturar relações não lineares.
Inspirado no modelo atômico de Rutherford, idealizei uma arquitetura onde o núcleo central processa as informações principais e os neurônios orbitais refinam o sinal, simulando a dinâmica de elétrons. Essa abordagem permite tanto aprendizado eficiente quanto uma representação visual intuitiva do fluxo de dados.
2. Metodologia
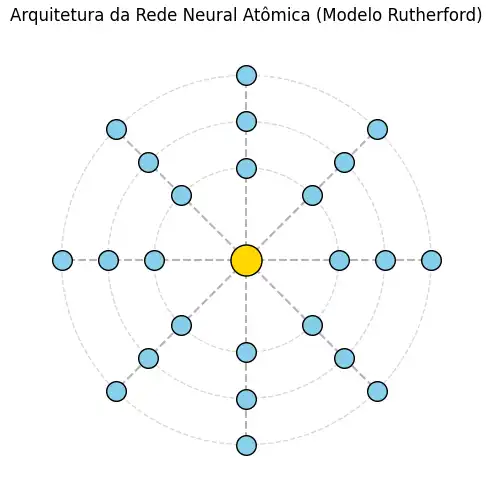
2.1 Arquitetura da Rede Neural Atômica
A rede é composta por:
- Núcleo: recebe as entradas e gera uma representação central e 8 features.
- Órbitas: três camadas ocultas concêntricas que refinam a informação.
- Conexão de volta ao núcleo: mistura o núcleo com sinais orbitais, reforçando o processamento central.
- Saída: uma camada sigmoide que fornece a probabilidade da classe binária.
2.2 Conjunto de dados
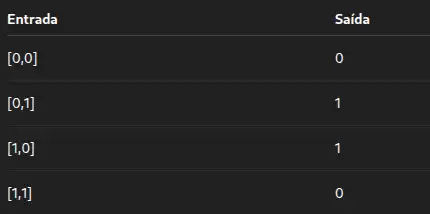
- Trata-se de um dataset pequeno e não linear.
- Ideal para testar a capacidade de aprendizado da rede.
2.3 Treinamento
- Função de perda: BCELoss (Classificação Binária)
- Otimizador: Adam com learning rate = 0.005.
- Número de épocas 10.000.
Durante o treinamento, a loss diminui gradualmente, indicando aprendizado.
3. Resultados
3.1 Saídas do modelo
Após o treinamento, a rede produz as seguintes saídas:
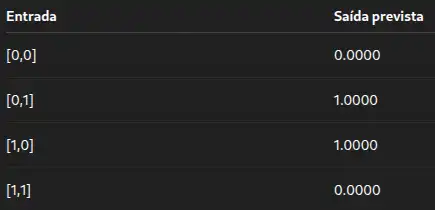
- A rede aprendeu corretamente a função XOR.
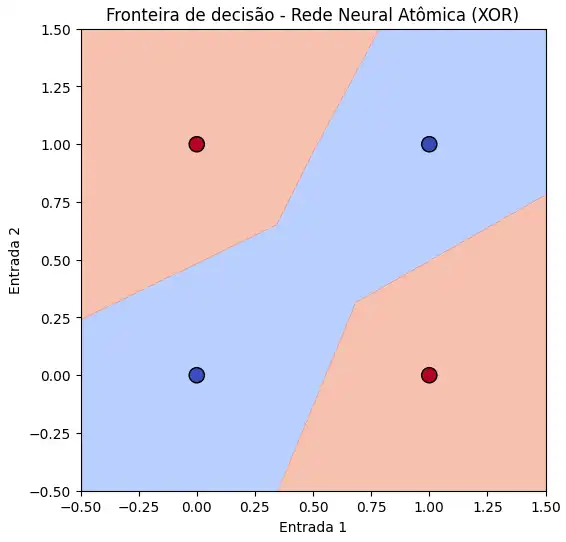
3.2 Fronteira de Decisão
- Azul: saída = 0
- Vermelho: saída = 1
- Pontos do XOR destacados, mostrando separação clara das classes.
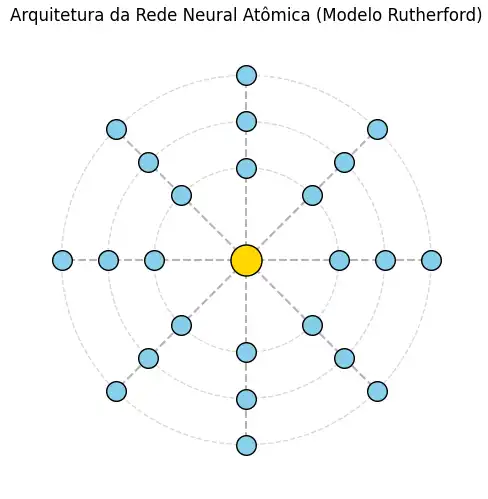
3.3 - Arquitetura Atômica
- Núcleo central dourado
- Neurônios em órbitas azuis
- Linhas conectando órbitas mostrando o fluxo de informações
4. Discussão
- Comparada a uma MLP tradicional, a rede oferece:
- Organização visual clara (núcleo + órbitas)
- Capacidade de aprendizado similar com arquitetura pequena
- Uma metáfora intuitiva do fluxo de informações
- Limitações: avaliada apenas com XOR para validar o modelo atômico; precisa de validação em datasets maiores.
- Potencial: ensino de redes neurais, visualização de fluxo, inspiração para novas arquiteturas.
5. Conclusão
A Rede Neural Atômica resolve o XOR perfeitamente.
Oferece representação visual intuitiva, facilitando o entendimento do processo interno.
Abre caminho para explorar arquiteturas inspiradas em conceitos físicos e químicos.
6. Referências
- Goodfellow, I., Bengio, Y., Courville, A. Deep Learning. MIT Press, 2016.
- Rutherford, E. Modelo atômico de Rutherford, 1911.
- Artigos clássicos sobre XOR e redes neurais de camada única.
7. Apêndice: Código Completo
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
# ======================
# Classe Rede Atômica
#=======================
class AtomicNN(nn.Module):
def __init__(self, input_dim = 2, hidden_dim = 8, output_dim = 1):
super(AtomicNN, self).__init__()
self.nucleus = nn.Linear(input_dim, hidden_dim)
self.orbit1 = nn.Linear(hidden_dim, hidden_dim)
self.orbit2 = nn.Linear(hidden_dim, hidden_dim)
self.orbit3 = nn.Linear(hidden_dim, hidden_dim)
self.nucleus_back = nn.Linear(hidden_dim, hidden_dim)
self.output = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
core = torch.relu(self.nucleus(x))
orbit1 = torch.relu(self.orbit1(core))
orbit2 = torch.relu(self.orbit2(orbit1))
orbit3 = torch.relu(self.orbit3(orbit2))
fusion = torch.relu(self.nucleus_back(orbit3) + core)
out = torch.sigmoid(self.output(fusion))
return out
# =====================
# Classe POO principal
# =====================
class AtomicXor:
def __init__(self, epochs = 10000, lr = 0.005):
# Dados XOR
self.X = torch.tensor([[0, 0], [0, 1], [1, 0], [1, 1]], dtype = torch.float32)
self.Y = torch.tensor([[0], [1], [1], [0]], dtype = torch.float32)
# Modelo
self.model = AtomicNN()
# Hiperparâmetros
self.epochs = epochs
self.lr = lr
# Critério e otimizador
self.criterion = nn.BCELoss()
self.optimizer = optim.Adam(self.model.parameters(), lr = self.lr)
# Treinar
def train(self):
for epoch in range(self.epochs):
self.optimizer.zero_grad()
outputs = self.model(self.X)
loss = self.criterion(outputs, self.Y)
loss.backward()
self.optimizer.step()
if (epoch + 1) % (self.epochs//5) == 0:
print(f'Época {epoch + 1}, Loss: {loss.item():.4f}')
# Testar
def test(self):
with torch.no_grad():
preds = self.model(self.X)
print('\nSaída final da rede atômica (XOR):')
for i in range(len(self.X)):
print(f'{self.X[i].tolist()} -> {preds[i].item():.4f}')
return preds
#Plotar fronteira de decisão
def plot_decision_boundary(self):
xx, yy = np.meshgrid(np.linspace(-0.5, 1.5, 200), np.linspace(-0.5, 1.5, 200))
grid = torch.tensor(np.c_[xx.ravel(), yy.ravel()], dtype=torch.float32)
with torch.no_grad():
Z = self.model(grid).reshape(xx.shape)
plt.figure(figsize = (6, 6))
plt.contourf(xx, yy, Z, levels = [0, 0.5, 1], cmap = 'coolwarm', alpha = 0.6)
X_plot = self.X.numpy()
Y_plot = self.Y.numpy().flatten()
plt.scatter(X_plot[:,0], X_plot[:,1], c = Y_plot, cmap = 'coolwarm', edgecolors = 'k', s = 120)
plt.title('Fronteira de decisão - Rede Neural Atômica (XOR)')
plt.xlabel('Entrada 1')
plt.ylabel('Entrada 2')
plt.show()
# Plotar arquitetura atômica
def plot_atom_architecture(self):
fig, ax = plt.subplots(figsize = (6, 6))
ax.set_aspect('equal')
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
ax.set_title('Arquitetura da Rede Neural Atômica (Modelo Rutherford)')
# Cores
core_color = 'gold'
orbit_color = 'skyblue'
# Núcleo
nucleus_pos = (0, 0)
ax.scatter(*nucleus_pos, s = 500, c = core_color, label = 'Núcleo', edgecolors = 'k', zorder = 5)
# Função para distribuir neurônios em órbitas
def draw_orbit(radius, n_neurons):
angles = np.linspace(0, 2 * np.pi, n_neurons, endpoint = False)
positions = [(radius * np.cos(a), radius * np.sin(a)) for a in angles]
for pos in positions:
ax.scatter(*pos, s = 200, c = orbit_color, edgecolors = 'k', zorder = 5)
circle = plt.Circle(nucleus_pos, radius, color = 'gray', fill = False, linestyle = '--', alpha = 0.3)
ax.add_artist(circle)
return positions
# Desenha 3 órbitas
orbit1_pos = draw_orbit(2, 8)
orbit2_pos = draw_orbit(3, 8)
orbit3_pos = draw_orbit(4, 8)
#Linhas conectando núcleo à primeira órbita (simplificado)
for pos in orbit1_pos:
ax.plot([nucleus_pos[0], pos[0]], [nucleus_pos[1], pos[1]], 'k--', alpha = 0.3)
#Linhas entre órbitas (Simplificado)
for pos1, pos2 in zip(orbit1_pos, orbit2_pos):
ax.plot([pos1[0], pos2[0]], [pos1[1], pos2[1]], 'k--', alpha = 0.3)
for pos2, pos3 in zip(orbit2_pos, orbit3_pos):
ax.plot([pos2[0], pos3[0]], [pos2[1], pos3[1]], 'k--', alpha = 0.3)
plt.axis('off')
plt.show()
# ==========================
# Função main
# ==========================
if __name__ == '__main__':
atomic_xor = AtomicXor(epochs = 10000, lr = 0.005)
atomic_xor.train()
atomic_xor.test()
atomic_xor.plot_decision_boundary()
print('\n')
atomic_xor.plot_atom_architecture()





