Linearização para Regressão Linear
- #Python
Introdução
Linearização é uma técnica muito útil para transformar dados não lineares em naqueles que se comportem como uma linha reta. Cabe já falar que devemos sempre tomar cuidados matemáticos muito importantes, que se forem esquecidos, as nossas regressões nos retornarão valores errados. Sem mais delongas vamos entender a linearização.
Linearização: quando fazer?
Em cursos onde se realizam bastantes análises experimentais, como física, que é o meu caso, utiliza-se bastante a técnica de linearização. Esta técnica permite realizar a regressão linear e obter os resultados, que no caso da física são valores dos coeficientes que tem sentido físico. A própria aceleração da gravidade é “medida” desta forma, e este é um assunto para outro momento.
O momento que devemos realizar a linearização dos dados é quando soubermos que os dados não seguem uma tendência linear. Para obter essa informação temos algumas opções:
1 — Conhecemos a equação que representa o evento observado
2 — Observamos graficamente a relação entre a variável dependente em função da variável independente
3 — Fazemos a regressão linear e testamos.
Aqui focarei na alternativa 2 que é mais abrangente. Para tal temos que observar a tendência dos dados. Uma tendência linear tem o padrão do gráfico à esquerda, enquanto a tendência da equação que usamos de exemplo é do gráfico a direita. Basicamente, se o gráfico entre as variáveis não tem tendência linear, então a linearização pode ser utilizada. Fica aqui a importância da análise exploratória antes de realizar o Machine learning.
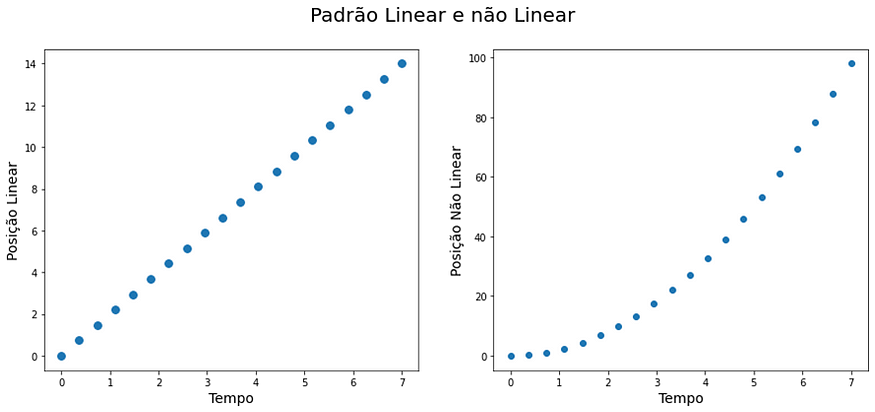
Linearização: como fazer?
2 — Logaritmo
O logaritmo é a melhor forma para linearizar, isto porque não precisa saber qual a equação que governa as relações entre os dados. Você admite que é uma multiplicação entre os dados e calcula o logaritmo. Quando você fizer isso os dados serão linearizados por causa das propriedades do logaritmo. Segue o exemplo no python.
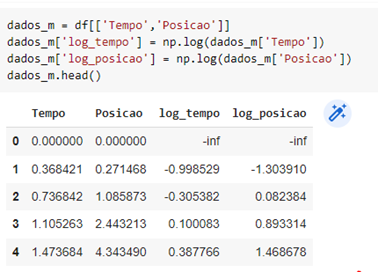
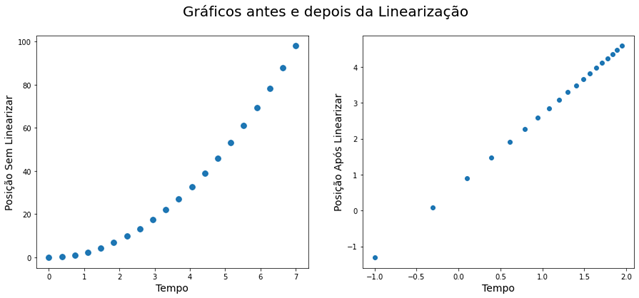
Para esta técnica devemos nos preocupar com os dados passados e com os dados que serão previstos. A regressão linear é testada em cima dos dados da linearização, que são logaritmos dos dados obtidos, por isso devemos passar o logaritmo dos dados desejados para realizarmos nossa previsão. E o valor que vamos receber de previsão também é o logaritmo. Para obtermos o valor explicitamente sem o logaritmo devemos realizar a operação contrária do logaritmo, que é a exponenciação. Se você utilizou, como eu, np.log para calcular o logaritmo bastar elevar seu valor previsto usando np.e.
Conclusão
Apresentei duas formas de realizar linearizações, e que podem ser muito úteis para o seu dia a dia analisando dados. É preciso não esquecer a matemática para fazer as linearizações, pois assim também deixaremos de lado as questões que devemos lidar no momento de obter nossos valores previstos da regressão.
Devo dizer que omiti aqui a diferença entre np.log e np.log10, dois métodos do numpy. Esta discussão será deixada para outra publicação. Até lá sinta-se a vontade para testar as técnicas de linearização e ver como fiz essas técnica de forma bem simples no meu notebook.
Segue meu github e minha despedida, até a próxima!
Algumas referências e sugestões de leitura



