Complexidade Quadrática O(N²)
- #GoLang
package main
import (
"fmt"
)
func printaTodosOsPares(n int) {
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
fmt.Println(i, j)
}
}
}
Acabamos de falar sobre um caso onde temos dois for e a complexidade era O(n) mas esse caso é diferente pois o for é aninhado e não é como se fosse um caso de N * 2 é N ao quadrado, se N fosse 10 o retorno seria 100 a proporção em que o tempo de execução cresce é muito maior.
Enquanto a complexidade linear sobe em uma linha reta, a complexidade quadrática sobre em uma curva, chamada de parábola, em relação ao eixo de tempo, para cada vez que N aumenta.
Nesse caso a regra de pensar quem domina quem também é válida, se vc tiver dois for aninhado e um solto dentro da função vc não tem um O(n + n²) porque o N linear é insignificante perto do quanto N² cresce. Então no final conte apenas com a maior função, O(n²). Lembrando novamente que big O é sobre o comportamento quando a entrada cresce muito. Um algoritmo linear pode ser pior que um quadrático até certo ponto, justamente por causa das constantes. Em algum momento o quadrático vai ficar mais lento, mas e se o ponto que isso acontece for lá quando a entrada tiver mais de 500 terabytes? Vale a pena usar o linear? Mas não se preocupe, para algoritmos simples e na maior parte dos casos que se usa no mercado de software, o ponto onde o O(n²) fica mais lento é bem cedo. Mas conhecimento nunca é demais =)
Output:
00
01
10
11
Com um parâmetro de 2 esse seria o output, porque o índice i varia de 0 a n para cada um dos valores de j. O número de cálculos vai ser uma multiplicação deles, ao invés da soma, ou seja, vai ser bem mais coisa pra parâmetros maiores.
Existem também a Complexidade Cúbica O(n³) seriam três loops aninhados a lógica é a mesma, não pretendo abordar sobre ele por aqui mas aqui vai um exemplo:
package main
import (
"fmt"
)
func main() {
var k, l, m int
var arr [10][10][10]int
for k = 0; k < 10; k++ {
for l = 0; l < 10; l++ {
for m = 0; m < 10; m++ {
arr[k][l][m] = 1
fmt.Println("Valor do elemento", k, l, m, " é", arr[k][l][m])
}
}
}
}
Temos três loops percorrendo um array multidimensional a complexidade aumenta tanto que pra percorrer esse array com três loops são precisas mil operações pois 10 x 10 x 10 = 1000. Se o tamanho do array aumenta, o número de operações aumenta muito, mas muito mais.
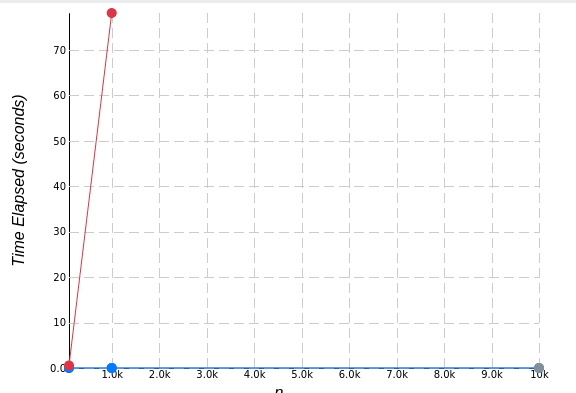
Agora dá pra ter uma ideia da perspectiva, veja como a linha vermelha de uma complexidade quadrática sobre em relação as outras e também como a complexidade linear parece plana em relação a quadrática. De repente aqueles 18 segundos não são nada comparados a mais de 1 minuto isso com um input de 10kb. Então se eu tivesse no mesmo algoritmo essas três complexidades pouco importa se o O(n) vai receber 1tb de input o que ta te ferrando é essa O(n³), por isso nos preocupamos apenas com a maior função em relação a Big O Notation, aquela que domina as outras à medida que a entrada vai crescendo, e fazem elas parecerem insignificantes.
Algumas ideias pra você calcular as operações com Big O
- Operações aritméticas são sempre constant time (os algoritmos de aritmética em si não são, mas nós consideramos que sim)
- Atribuições de variáveis são constant time
- Acessar elementos de array por index ou objetos por chave é constant time, enquanto acessar elementos de linked lists (como a do python) é linear time.
- Em um loop a complexidade é o tamanho do loop * a complexidade do que tiver dentro do loop
Não precisa decorar mas é bom saber. As complexidades quadrática e cúbica são chamadas de polinomial. Todo algoritmo com complexidade n elevado a uma constante (2, 3, 4, 5, 6, etc) é polinomial. Se o algoritmo tiver complexidade n elevado à alguma variável que também cresce com a entrada (por exemplo, uma força bruta para o algoritmo do caixeiro-viajante ou quebrar senhas), então é o algoritmo é exponencial, a pior e mais lenta das complexidades.