Complexidade Algoritmica
- #GoLang
Quando se começa a programar tem um momento durante o aprendizado em que você tem um “click” você começa a pensar nos problemas do ponto de vista de um programador. Não tem mais volta, você está fadado ao resto da vida a olhar para um interruptor e pensar:
if interruptor == up {
turnLightOn()
} else {
turnLightOff()
}
Parece que o cérebro funciona com lógica boleana, só que não, você levou muito tempo para que em determinado momento a sua cabeça se voltasse para as coisas dessa forma, isso é a construção de muito trabalho, ao mesmo tempo parece que foi sim um “click”, isso porque não percebemos a nós mesmos com muita clareza.
Um dos “clicks” que ainda podem acontecer ou já aconteceu com você, é quando temos um determinado problema e para resolvê-lo deixamos de pensar assim: “Como posso resolver isso?”
Para pensar assim: “Já sei como resolver, mas essa solução é suficiente?” ou “ela é escalável ou legível?”.
Até conseguimos resolver problemas, porém quando somos iniciantes e todo desafio proposto parece complicado nossa única preocupação é apenas resolver da forma que for possível. A mudança aqui é quando já temos bagagem em resolver problemas, só que agora levamos menos tempo e temos o privilégio de pensar em uma implementação diferente.
Acho aceitável uma solução não escalável em um cenário onde se é iniciante, não cobraria isso de alguém que é um estagiário por exemplo, nem daria acesso a ele pontos do sistema que possam ser críticos.
Não quero ser o cara que fala “se você não sabe Estrutura de Dados e Algoritmos você é mal programador”, mas se você quer ter um segundo “click” e começar a ver a programação sob mais uma perspectiva recomendo muito que estude sobre.
COMPLEXIDADE DE ALGORITMOS
A complexidade de um algoritmo é analisada em termos de tempo e espaço. Normalmente, o algoritmo terá um desempenho diferente com base no processador, disco, memória e outros parâmetros de hardware. A complexidade é usada para medir a velocidade de um algoritmo. Sendo o Algoritmo um agrupamento de etapas para se executar uma tarefa. O tempo que leva para um algoritmo ser concluído é baseado no número de passos.
Digamos que um algoritmo percorre um array de dez posições somando o índice das posições a 200.
A complexidade seria de 10 X T, sendo que T representa o tempo necessário para atualizar todos os elementos do array com a operação de soma. Como cada computador pode ser muito diferente um do outro isso varia de acordo com o hardware, a linguagem utilizada e o sistema operacional.
package main
import "fmt"
func main() {
var arr [10]int
for indice := 0; indice < len(arr); indice++{
arr[indice] = indice + 200
fmt.Printf("indice[%d] = %d\n", indice, arr[indice])
}
}
Output:
indice[0] = 200
indice[1] = 201
indice[2] = 202
indice[3] = 203
indice[4] = 204
indice[5] = 205
indice[6] = 206
indice[7] = 207
indice[8] = 208
indice[9] = 209
Temos 10 operações acontecendo, aparentemente muito simples.
Com uma Notação é possível calcular a complexidade de um algoritmo sem precisar levar em consideração parâmetros de hardware.
BIG O NOTATION
A Big O Notation é uma notação especial que indica a complexidade de um algoritmo. Na realidade existem várias notações: big e small O, big e small omega e theta. A notação do O é sobre “limite por cima”, a omega sobre “limite por baixo” e a theta é a combinação de ambos. Os ‘small’ representam afirmações mais rígidas sobre a complexidade do que os ‘big’. Geralmente a big O é mais utilizada porque o interesse é verificar o máximo de recursos que o algoritmo vai utilizar, sem tanta rigidez, e então tentar reduzir isso, quando possível.
A função de tempo T(n) representa a complexidade do algoritmo onde T(n) = O(n) afirmando que um algoritmo tem uma complexidade linear de tempo. Pois o TEMPO é completamente relacionado a N o tamanho de input do algoritmo (e às vezes também outros aspectos).
Geralmente a maioria do material relacionado a Big O é formal demais, talvez isso afaste um pouco as pessoas mas com um pouquinho de dedicação a gente consegue enxergar os padrões.
Em Big O Notation as complexidades de tempo linear, logarítmica, cúbica e quadrática são representações de complexidades diferentes de relação entre T e N em um algoritmo. A Big O Notation também é usada para, determinar quanto espaço é consumido pelo algoritmo.
Então você pode visualizar de forma gráfica como funciona o crescimento de tempo e de tamanho do input e como eles se relacionam. No final é sobre isso, a relação entre um ou mais aspectos da entrada e o tempo de execução do algoritmo. Importante: nem sempre o desempenho do algoritmo é afetado apenas pelo tamanho da entrada. O algoritmo de ordenação counting sort, por exemplo, é afetado também pelo maior número na lista.
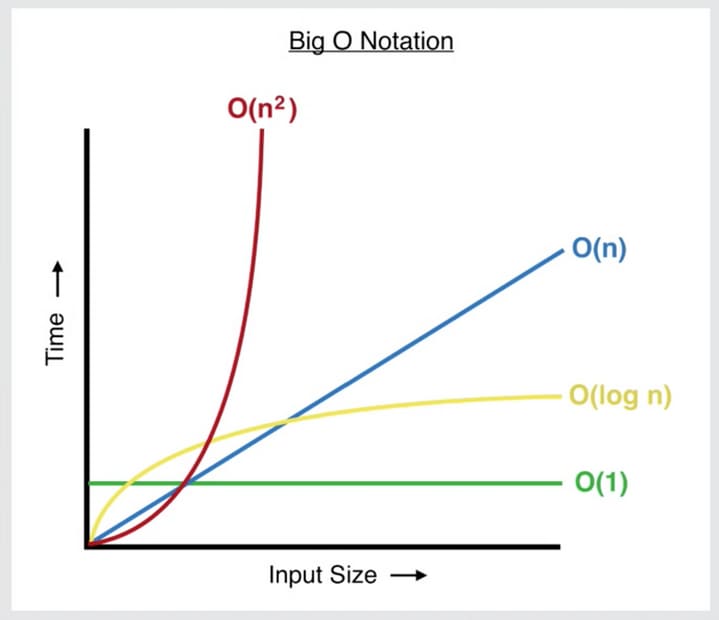
Vou falar sobre as principais funções de complexidade, e pretendo dar maior enfase na complexidade de tempo, mais tarde assuntos como recursão vão aparecer então vou diluindo isso durante o processo. Você pode estar se perguntando “ok mas como eu calculo isso?” como eu descubro a complexidade do meu algoritmo? Isso você descobre no próximo artigo.
https://web.digitalinnovation.one/articles/constantes-o1?back=%2Fhome&page=1&order=oldest



